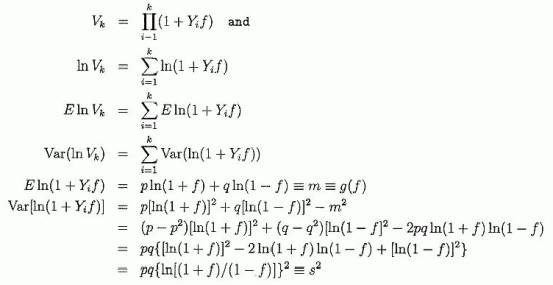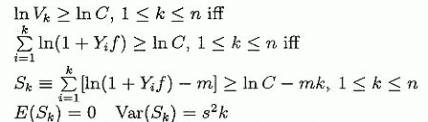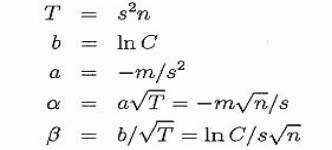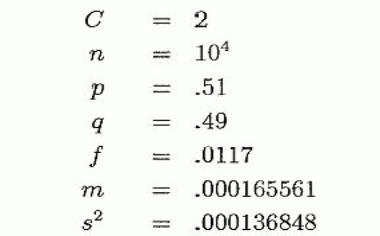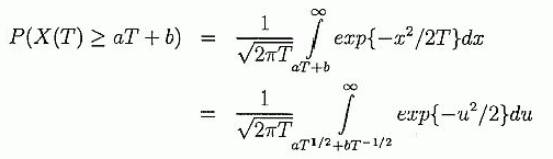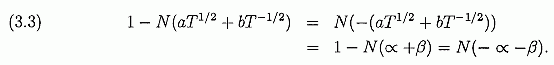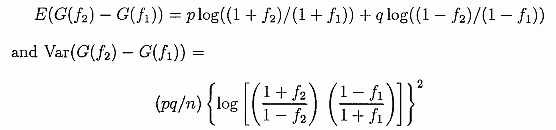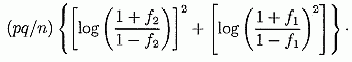КРИТЕРИЙ КЕЛЛИ В БЛЭК ДЖЕКЕ, ТОТАЛИЗАТОРЕ И НА РЫНКЕ АКЦИЙ
THE KELLY CRITERION IN BLACKJACK, SPORTS BETTING, AND THE STOCK MARKET Edward O. ThorpЧасть 2
Оптимальный рост: формулы критерия Келли для практиковТак как критерий Келли асимптотически максимизирует ожидаемую норму роста капитала, он часто называется стратегией оптимального роста. Интересно сравнить его с другими стратегиями фиксированных долей. Я представлю некоторые результаты, которые нахожу полезными практически. Я хочу постараться объяснить все это просто и понятно. Эти результаты явились результатом размышлений об "интересных вопросах". Я не делал полную литературную выборку, но я знаю, что похожие результаты были уже представлены математической общественности. См. например. Браун (1995, 1996) и дальнейшие ссылки.
(a) Вероятность достижения установленной цели за n попыток.Давайте сначала побросаем монету. Мы отмечаем, что результат похож на обычное Броуновское движение. Howard Tucker обратил на это мое внимание еще в 1974 году, и это, вероятно наиболее полезный отдельный факт из всех, что я знаю, имея дело с разнообразными проблемами азартных игр и с теорией финансовых производных. Для стандартного Броуновского движения X (t) мы имеем
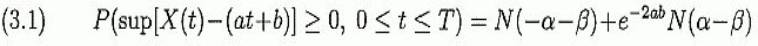 где α=а√Т, а β =b/√T. См. Рисунок 2. В нашем приложении а < 0, b > 0, так что мы ожидаем limT→∞ P(X(t) ≥ at + b, 0 ≤ t ≤ T)=1. Пусть f будет долей ставки. Примем независимые тождественно распределенные (i.d.d..) попытки Yi, i=1..., n, при P (Yi=1)=p > 1/2, P (Yi =-1)=q < 1/2; также примем p < 1, во избежание тривиального случая p= 1. Установленная доля ставки f, 0 < f < 1, в каждой попытке. Пусть Vk будет величина капитала игрока или инвестора через k попыток, с начальным значением V0. Выберем начальную ставку Vo= 1 (без потери общности); число попыток n; цель С > 1. Какова вероятность того, что Vk ≥ С для некоторого k, 1 ≤ k ≤ n? Она та же самая, как вероятность, что log Vk; ≥ log C для некоторого k, 1 ≤ k ≤ n. Допустив ln=loge, мы имеем:
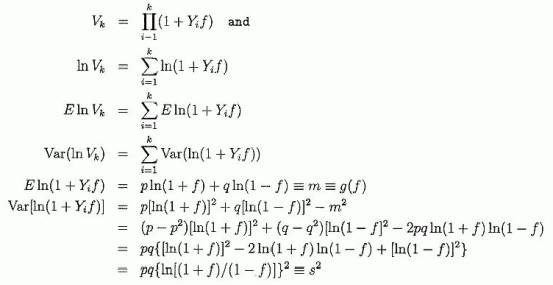 Смещение за n попыток: nm Изменение за n попыток: s2n 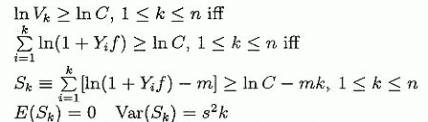
Нам нужна вероятность Ргob(Sk ≥ ln C - mk, 1 ≤ k ≤ n). Теперь мы используем нашу формулу Броуновского движения, чтобы приблизить Sn Prob (X(t) ≥ lnС - Хt/s2, 1 ≤ t ≤ s2n) где каждое значение Sn приближено к X(t), сдвиг 0 и изменение s2 (0 ≤ t ≤ s2, s2 ≤ t ≤ 2s2..., (n - 1)s2 ≤ t ≤ ns2). Обратите внимание: приближение "хорошо" только для "больших" n. Тогда в первоначальной формуле (3.1): 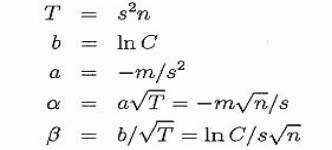
Пример 3.1 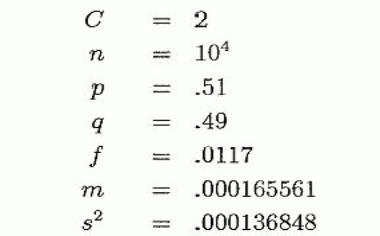 Тогда P(·)=0.9142 Пример 3.2 Повторим с f =0.02 тогда m=0.000200013 s2 =0.000399947 а P(∙)=0.9214
(b) Вероятность того, что начальный капитал когда-либо уменьшится
до доли xЭто вопрос, который причиняет много волнений игрокам и инвесторам. На него можно ответить, хотя бы приблизительно, нашими предыдущими методами. Используя заметки предыдущего раздела, мы хотим P (Vk ≤ x для некоторых k, 1 ≤ k ≤ ∞). Подобные методы выдают (намного проще) формулу непрерывного приближения: Prob (·)=e2ab, где a =- m/s2, а b=- ln x, что можно записать, как (3.2) Prob (·)= x^(2m/s2) где ^ означает экспоненту. Пример 3.3. p=0.51 f=f* =0.02 2m/s2=1.0002 Prob(·) =x Мы увидим в разделе 7 что для ограниччения непрерывного приближения и оптимальной доли Келли f*, Р (Vk (f *) ≤ x для некоторых k ≥ 1)=x. Мой опыт показывает, что большинство осторожных игроков или инвесторов, которые используют Келли, находят частое и существенное сокращение капитала излишне неудобным. Теперь мы можем видеть, почему. Чтобы уменьшить это, они предпочитают ставить несколько меньше чем рекомендуемая доля ставки f*. Это также повышает уровень безопасности в случае, если игровые ситуации менее благоприятны, чем ожидалось. Потери из-за уменьшенном роста капитала не является серьезными для умеренной «недоставки». Мы обсудим это позже, в разделе 7.
(с) Вероятность попадания в или выше указанной величины
в конце определенного числа попыток.Доктор Richard Hecht (1995) предложил отрегулировать эту вероятность в качестве цели и использовал для этого компьютерный метод определения оптимальной (в соответствии с этим критерием) фиксированной доли для p - q= 0.02 и различных с, n и определенных вероятностей успеха. Это - намного более легкая проблема чем похожее зондирование (a). Для вероятности того, что X(T) в конце концов превысит цель, мы имеем:
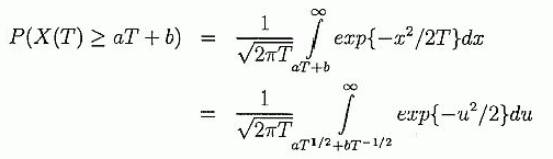
где и=x/√T так что x=aT +b дает u√T =aT + b и U=aT1/2-bT-1/2. Интеграл равен
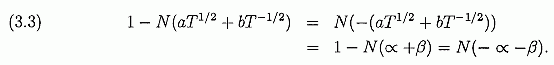 Например (3.1) f =.0117 и P= .7947. Например (3.2) P=.7433. Пример (3,3) - для оптимальной доли Хечта, а пример (3,2) - для оптимальной доли Kelly, Обратите внимание на различие значений P. Наши числовые результаты совпадают с моделированием Хечта в проверенных нами случаях. Браун (1996) дал изящное решение проблемы непрерывного приближения: Какая стратегия максимизирует вероятность достижения установленной цели С к или до указанного времени n и какова соответствующая вероятность успеха? Обратите внимание, что оптимальная стратегия включает изменение доли ставки в зависимости от оставшегося времени и расстояния до цели, Как экстремальный пример, только чтобы сделать пометку, предположим, что n=1 , а C=2. Если X0 < 1, то никакая стратегии не сработает и вероятность успеха равна 0. Но, если 1 ≤X0 ≤ 2, нужно делать ставку по крайней мере 2 - X0, таким образом любая доля f ≥ (2 — X0)/X0, для вероятности успеха p. Еще экстремальный пример: n=10, С= 210 =1024, X0=1. Здесь единственная стратегия, которая может преуспеть, состоит в том, чтобы делать ставку f=1 в каждой попытке. Вероятность успеха равна p10 для этой стратегии и 0 для всех других (если p < 1), включая Келли.
(d) Непрерывное приближение времени, ожидаемого
для достижения цели.Согласно Теореме l (v), стратегия оптимального роста асимптотически минимизирует ожидаемое время достижения цели. Вот что это означает. Предположим для цели С что m(C) - самый большой нижний предел ожидаемого времени достижения C из всех стратегий. Предположим, t* (C) - ожидаемое время при использовании стратегии Келли. Тогда limC→∞ (t*(c)/m(c))= 1, Непрерывное приближение к ожидаемому числу попыток для достижения цели C > X0=1 будет (3.4) n(C,f)=(lnC)/g(f) где f - любая стратегия фиксированной доли. Происхождение - в приложении III. Теперь g(f) имеет уникальный максимум на g(f*) так, что n(C, f) имеет уникальный минимум на f=f*. Кроме того, мы можем увидеть, насколько дольше, в среднем, придется добираться до С при отклонении от f*.
(e) Сравнение стратегий с фиксированной долей: вероятность,
что одна стратегия опередит другую после n попыток. Теорема 1 (iv) говорит, что капитал, при использовании стратегии Келли будет стремиться, в конечном счете, к бесконечно большому приумножению богатства, используя любую "существенно иную" стратегию. Можно показать, что любое фиксированное f ≠ f* - это "существенно иная" стратегия. Это приводит нас к вопросу о том, насколько стратегия Келли опережает другую стратегии фиксированной доли, и шире говоря, как быстро одна стратегия фиксированной доли опережает (или отстает) другую. Если Wn - число побед за n попыток, а n — Wn - число проигрышей, то G(f)=(Wn/n) ln (l + f) + (1 - Wn/n) ln (1 - f) это фактически (случайная переменная) коэффициент роста. Как мы видели, его ожидание (3.5) g(f)=E(G(f)}=p log(1 + f) + qlog(1 - f) а разница G(f) - 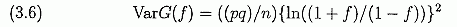 ТО из этого следует, что G(f), который имеет форму G(f)==a(∑Tk)/n + b, приблизительно обычно распределяется со средней g(f) и вариантом Va.rG(f). Это позволяет нам дать распределение Xn и еще раз ответить на вопрос в 3(c). Проиллюстрируем это на примере. Пример 3,3 p=0.51 q=0.49 f*=0.02 N=10,000 и s= стандартное отклонение G(f) 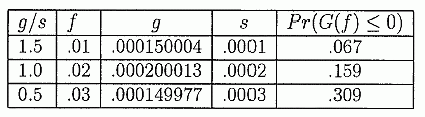 Продолжая, находим распределениеG(f2) - G(f1). Мы рассматриваем два случая. Случай 1. Та же самая игра. Здесь мы предполагаем, что оба игрока делают ставки на одни и те же попытки, например, на монету, или на одинаковые сдачи в блэк джеке, или на одно и то же на тотализаторе. На рынке акций, оба игрока могут вкладывать в одну и ту же акцию одновременно. Мы находим
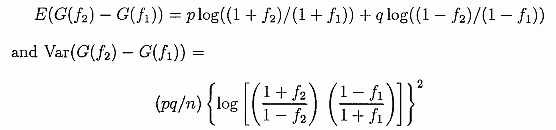 где G(f2) — G(f1) приблизительно нормально распределяется по среднему и варианту. Случай 2. Одинаково распределенные независимые игры. Это соответствует ставкам на два различных ряда бросков одной и той же монеты.E(G(f2) — G(f1)) - как и прежде. Но теперь Varг(G(f2) — G(f1)) =Vаг(G(f2))+Var(G(f1)) потому что G(f2) и G(f1) теперь независимы. Таким образом Var(G(f2) — G(f1))= 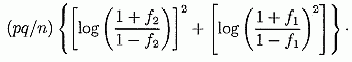 Пусть 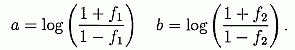 Тогда в случае 1, V1=(pq/n)(a - b)2 а в случае 2, V2 =(pq/n)(a2 + b2) и a, b > 0, V1 < V2 как и ожидалось. Мы можем теперь сравнить стратегию Келли с другими фиксированными долями, чтобы определить вероятность лидерства Келли после n попыток. Обратите внимание, что эта вероятность всегда больше 1/2 (с точностью непрерывного приближения, которое является приближением биноминального распределения нормали, с его известными и полностью изученными свойствами) потому что g(f*) — g(f) > 0 где f*=p — q и f ≠ f* - некоторая альтернатива. Это может не быть истинным для малых n, с бедным приближением. Как экстремальный пример, если n=1, любое f > f* побеждает Келли с вероятностью p > 1/2. Если вместо этого n=2, f > f* побеждает с вероятностью p2 и p2 > 1/2, если p > 1/√2 =0.7071. Так, f < f* выигрывает с вероятностью 1 - p2 и 1 - p2 > 1/2 если p2 < 1/2, i.e. p < 1/√2 =0.7071. Итак, когда n=2, Келли всегда теряет больше половины времени к некоторому другому f если p= 1/√2. Теперь у нас есть формулы, с которыми мы можем исследовать много практических применений критерия Келли.
© Edward O. Thorp
Оригинал статьи (на английском)
Перевод 2001 г. Investo.ru
|