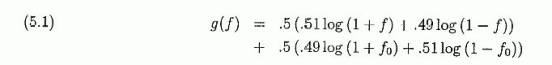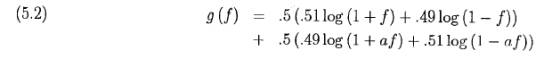Несколько позже John
Leib написал несколько статей на форуме
по Блэк джеку с критикой
критерия Келли. Он был очень смущен
на "длинной дистанции". Что это
и когда оно происходит?
Начнем с примера,
Пример
4.1 p=0.51, n=10,000
Vi
и si, i=1,2 разница и стандартное
отклонение, соответственно, для Случаев 1
и 2, а R=V2/V1
=(a2 + b2)/(a-b)2 так,
что s2=S1√R.
Таблица 4.1 суммирует некоторые результаты. Мы
можем также приближать √R
со степенью, используя лишь первое приближение a
и b: a=2f1,
b=2f2 так
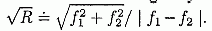
Приближенные результаты будут,
соответственно, 2.236, 3.606, и 1.581.
ТАБЛИЦА 4.1. Сравнение стратегий
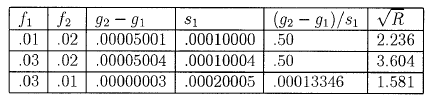
Первые два
ряда показывают, как почти симметрично ведет себя
каждая сторона оптимального
f*==.02. Колонка (g2—g1)/S1
показывает нам, что f*
=.02 только при стандарном отклонении
0.5 дает преимущество над соседними
f =.01 и f=.03
после n=10,000 попыток.
Теперь преимущество пропорционально
√n, колонка
(g2—g1)/s1
из таблицы 4.1 показывает
результаты таблицы 4.2:
ТАБЛИЦА 4.2 Долгосрочный пробег: (g2—g1)/s
после n попыток.

Фактор √R
из таблицы 4.1
показывает, насколько медленнее f2
доминирует над f1
в случае 1 по сравнению со случаем 2. Отношение (g2—g1)/S2
в √R
раз больше. Когда в
реальном мире сравнивают
стратегии, из практических
соображений чаще для
сравнения используют Случай 2 чем случай
1, превосходство f* в
дальнейшем затеняется.
Пример - игроки с различными долями ставок в блэк
джеке. Случай 1 соответствует ставкам на той
же самой последовательности сдач карт. Случай 2
выражает игру за разными
столами (поэтому Случай 2
становится независимым).
(Из-за положительной корреляции между
призами на сдачах, сыгранных
за одним и тем же столом, это промежуточное
состояние между Случаем 1 и Случаем 2.)
Важно понять, что "долгий срок ",
то есть время, которое требуется, чтобы f * стало
доминировать над соседними с указанной вероятностью, может меняться
неограниченно. Каждое применение требует отдельного анализа. В таких
случаях, как в примере 4.1, где доминанта - "медленная ", можно было
поспорить, что использование f* - не существенно. Как
аргумент против этого, рассмотрите два броска монеты. В игре 1 ваше
преимущество - 1.0 %. В игре 2 - 1,1 %. При ставке, равной единице,
после n попыток разница в ожидаемом росте будет Е2 - Е1
=.001n со стандартным отклонением s около √2n
следовательно {Е2 - Е1)/s=.001√n/√2,
что является 1, когда n=2 * 106, Так что требуется два
миллиона попыток, чтобы иметь шанс в 84 % того, что результат игры 2 будет
лучше, чем результат игры 1. Это подразумевает несущественность выбора
игры с более высоким ожиданием?
Обсуждение игры в блэкджек в целом смотрите Thorp (1962, 1966);
Wong (1994) и Гриффин (1995). Критерий Келли
был применен для блэкджека Торпом (1962). Анализ более сложен, чем при
бросках монеты, потому что призы здесь не просто один к одному. В
особенности дисперсия – в целом больше 1, и доля Келли стремится быть
меньше, чем при подбрасывании монеты с
тем же самым ожиданием. Кроме того, распределение различных выплат зависит
от преимуществ игрока. Например частота сплитов, удвоений и блэкджеков
меняются по мере того, как изменяется преимущество. Вероятность нужного
приза, согласно ожидаемой ставке, находится решением уравнений Келли на
компьютере, может быть найдена стратегия, максимально близкая к
оптимальной.
Существуют некоторые примечательные концептуальные тонкости. Чтобы
проиллюстрировать их, мы упростим до модели броска монеты.
При каждой попытке мы имеем "благоприятную ситуацию" с вероятностью 0.5
при выигрыше или потере X единицы ставки, так что P [X= 1)
=0.51, P (X=·-1)=0.49 и с вероятностью 0.5 неблагоприятную
ситуацию с выигрышем или потерей У на единицу ставки, так что P (Y=
1)=0.49 и P (Y=-1) = 0.51. Прежде, чем ставить,
мы знаем, применяется X, или Y.
Предположим, игрок должен делать маленькие "ждущие" ставки в
неблагоприятных ситуациях, чтобы позднее иметь возможность эксплуатировать
благоприятные ситуации. На них он разместит "большие" ставки. Мы
рассмотрим два случая.
Случай 1. Ставим fo в неблагоприятных
ситуациях и находим оптимальное f *' для благоприятных ситуаций. Мы
имеем
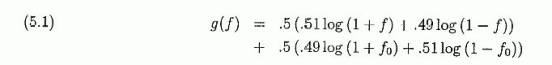
Так как второе выражение в (5.1) постоянно, f максимизирует
g(f), если
максимизировано первое выражение, так
f* =pi
- qi=
0.02, как обычно. Легко проверить что на всем спектре благоприятных
ситуаций работает тот же самый рецепт, f*i
=pi - qi
для I-той ситуации. И
опять, в ревльном блэкджеке f*i
былj бы
отрегулировано для несколько большей разницы. С дополнительным
ограничением типа fi ≤ kfo, где k
обычно множитель для fo выражающий спред ставки, принятый благоразумным
игроком, решение – всего только/; fi ≤
min (f*i
kfo,).
Любопытно, по-видимому подобная формулировка проблемы ставок ведет к
довольно разнящимся результатам.
Случай 2. Ставка f в благоприятных
ситуациях и af в неблагоприятных ситуациях, 0 ≤
a ≤ 1 .
Теперь размеры ставки в этих двух ситуациях связаны, анализ и
результаты становятся более сложными. Мы имеем норму роста Келли
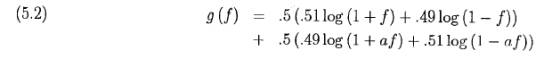
Если мы выбираем=0 (никаких ставок в неблагоприятных ситуациях), то
максимальная величина g(f)
будет около f*
=0.02, обычная доля Келли.
Если мы делаем "ожидающие ставки" величиной a > 0, то это сместит
значение f*
вниз, возможно, даже до 0. Ожидаемый рост, деленный на ожидаемую ставку
равен 0.02 (1 - a) / (1 + a), a ≥ 0. Если
a =0, мы получим
0.02, как и ожидалось. Если а - 1, мы получаем 0, как ожидалось:
это - справедливая игра, и доля Келли будет f*
=0. При увеличении от 0 до 1 (оптимальная) доля Келли f^
уменьшается от 0.02 до 0. Таким образом, доля Келли для благоприятных
ситуаций - меньше в этом случае, когда ставки при неблагоприятных
ситуациях уменьшают общее преимущество игры.
Arnold Snyder
обратил мое внимание на тот факт, что
Winston Yamashita (также)
сделал это (18 марта 1997) на страницах вебсайта Станфорда Вонга (Stanford
Wong).
В этом примере мы находим новый
f* для данной
величины a, 0 < a
< 1, решая
g' (f)=0. Значение
a=1/3, к
примеру, соответствует ставке 1/3 единицы при Y и 1 единице при X,
диапазон ставок от 3 до 1. Полное ожидание будет 0.01. Вычисления дают
f*=0.012001.
Таблица 5.1 показывает, как f* меняется с a.
Таблица 5.1 f* против
a

Чтобы понять, почему Случай 1 и Случай 2 имеет различные
f*, взглянем
сначала на уравнение (5.1). Часть
g(f)
соответствует неблагоприятным ситуациям, фиксирована, когда установлено
f0. Только часть
g(f),
соответствующая благоприятным ситуациям воздействует, изменяя
f, Таким образом,
мы максимизируем g(f)
только благоприятными ситуациями. Безотносительно к результату, тогда
уменьшается фиксированное количество части
g, содержащей
f0. С другой стороны, в уравнении (5.2) обе части
g{f) воздействуют
при изменении f,
потому что доля af, используемая для неблагоприятных ситуаций,
находится в постоянном отношении к доле
f, используемой в
благоприятных ситуациях. Теперь первый элемент, для благоприятных ситуаций,
имеет максимум на f= 0.02, и приблизительно "плоский" около. Но
второй элемент, для неблагоприятных ситуаций, является отрицательным и
уменьшается довольно быстро при
f=0.02. Также,
когда мы несколько уменьшаем
f, этот элемент
несколько увеличивается, в то время как первый элемент уменьшается лишь
очень незначительно. Здесь лежит
чистая выгода, так что мы находим
f*
< 0.02. Чем больше
a,
тем сильнее эффект этого элемента, тем сильнее мы должны уменьшить
f чтобы
получить f
*, как ясно показано в таблице 5.1. Когда есть спектр благоприятных
ситуаций, решение более сложно и может быть найдено через стандартные
мультипеременные методы оптимизации.
Более сложный Случай 2 соответствует тому, что серьезному игроку в
блэкджек, вероятно, нужно будет делать практически. Он должен будет
ограничить его текущую максимальную ставку до нескольких раз от его
текущей минимальной ставки. По мере того, как его капитал будет расти или
уменьшаться, соответственно пропорционально увеличиваются или уменьшаются
и размеры ставки.
© Edward O. Thorp
Оригинал статьи (на английском)
Перевод 2001 г. Investo.ru